
Exploring the timing and distribution effects of direct cardiac compression in a beating heart model
Introduction
Heart failure (HF) is a highly debilitating and progressive condition that afflicts tens of millions of people worldwide. Despite decades of research aimed at preventing and/or treating the underlying disease processes that lead to HF, the number of cases continues to rise at an alarming rate as the population ages. Indeed, among Americans 18 years and older, HF cases are projected to increase 46% from 2012 to 2030, with the total percentage of the population with HF expected to reach 2.97% (>8 million) in that same timeframe (1).
While medical therapies do exist, heart transplantation remains the only definitive treatment for end stage heart failure (2). Unfortunately, the donor pool has been—and continues to be—extremely shallow, limiting the number of patients who can receive this therapy to just a few thousand per year (3). Left ventricular assist devices (LVADs) can be used to help bridge the gap between donors and recipients. While useful, LVADs are not without their complications, with one of the most common and devastating being thromboembolic events (4,5). To address this problem, several groups have started to explore direct cardiac compression (DCC), a method of applying compression to the epicardial surface of the heart to augment cardiac output while avoiding blood contact (6-8). While LVADs treat the heart as a passive reservoir for blood, DCC interacts directly with the heart tissue. Thus, a key consideration in evaluating DCC performance are the myocardial mechanics caused by ventricular compression. These factors have not been examined to any significant extent to date due to the immense difficulty in measuring and calculating these metrics.
Our group has previously developed a framework for simulating and evaluating hemodynamic and biomechanical effects of DCC in a patient-specific beating heart model of heart failure (9-11). The aim of this study is to use this same modeling platform to simulate changes in compression patterns and timing for comparison with previous uniform compression simulations. These experiments represent the initial efforts to analyze the biomechanical effects of DCC.
Methods
Building upon our previous work, beating-heart simulations were created using a multiscale finite element analysis (FEA)software package (Continuity Pro, Insilicomed, La Jolla, CA) developed specifically for dynamic cardiac modeling. An in-depth description of software specifics has been published elsewhere (9,11). The essential elements of this in silico model and the methods used to simulate uniform and distributed cardiac compression profiles are summarized below.
Continuity Pro (CPro) is a multiscale cardiac modeling software package that combines cardiac geometry, cardiac fiber direction, calcium excitation-force coupling dynamics, and a lumped parameter circulatory model to simulate the action of a beating heart pumping blood through both systemic and pulmonary circulatory systems.
In this application, CPro was used to create a beating heart simulation unique to a specific patient, whose anatomic dimensions were deemed most typical (12,13). Note that patient specific models have been validated against the physiologic data that they were derived from (13). Simulated compressions were applied to this model as force boundary conditions that change as a function of time at the epicardial surface. Fixed boundary conditions at the epicardial base of the heart were applied to simulate the fibrous cardiac skeleton and valvular plain while also minimizing artifacts in the ventricular free walls. As with all previous studies, simulations were run at a constant heart rate of 80 beats per minute, with the aortic valve opening 146 ms after the start of the cardiac cycle. The timing of the cardiac phases is as follows: Isovolumetric contraction—0 to 146 ms, systolic ejection—146 ms to 300 seconds, isovolumetric relaxion—300 to 454 ms, diastolic filling—454 to 750 ms. Cardiac cycles were run until left and right ventricular stroke volumes (SVs) were within 5% of each other, indicating stable circulatory dynamics.
There are two experimental scenarios explored in this paper: (I) changing the compression from uniform to sequential from the apex to the base, and (II) applying uniform compression but changing its starting time with respect to the cardiac cycle. The maximum applied pressure to the left ventricle (LV) is 2.9 kPa and for the right ventricle (RV) is 0.46 kPa, consistent with our prior work (11). When percentages of the maximum load are described in the paper, it is with regards to the maximum applied pressure (e.g., a 50% maximum load corresponds to 1.45 and 0.23 kPa applied to the left and right ventricles respectively). A general outline of the two simulations is shown in Figure 1. Compression is applied during the systolic phases of the cardiac cycle. The general cadence for both is a parametric simulation followed by an analysis of the resulting hemodynamics, principal strain renderings, and regional fiber mechanical analysis. The fiber coordinates are relative to the starting orientation of the fibers, which changes transmurally. The three axes for the fiber components are the fiber direction (f), cross fiber direction (c), and transmural direction (t). These three directions give rise to the normal (ff, cc, tt) and shear (fc, ft, cf) strains.
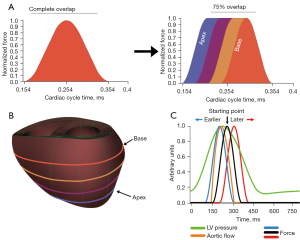
It is important to emphasize that these simulations build upon a previous parametric analysis of DCC (11). All prior simulations, as well as the ones presented here, apply DCC on the same initial heart failure model and take compressions from the parametric analysis and explore them temporally. This base failure model has a starting left and right ventricular ejection fraction of 15.3% and 24.8% respectively; all hemodynamics presented here are improvements from this initial starting point.
Sequential compression
Sequential compression is explored as the apex to base compression mimics how surgeons would apply manual cardiac compression (14). Moving from the initial uniform sinusoidal compression (Figure 1A), the circumferences of the model are sequentially compressed from the apex to the base of the heart (Figure 1A,1B). Uniform would entail compressing all four circumferences at once (blue, purple, yellow, and orange) whereas sequential would compress blue first and then purple, followed by yellow and finally orange. The compression profile for each circumference starts as a sinusoid but when the maximum force is reached, the force at that circumference is held constant. This occurs for each circumference until the most basal circumference reaches max force, at which point the applied force on all circumferences decreases sinusoidally, mimicking manual cardiac compression. The degree of how sequential the compressions are applied is determined by the overlap of the sinusoids. It is important to note that this overlap is based purely on time to max compression, such that time delays between circumferences is 30, 40, and 50 ms for 75%, 50%, and 25% overlap respectively. Simulations were run at 50% of the maximum load for 75%, 50%, and 25% overlap. The hemodynamic results for each degree of overlap were analyzed. From our past work, we found that applying normalized forces greater than 70% elicited unique fiber dynamics in which an exponential increase in principal strain occurred once forces exceeded 70% of the maximum load. To probe this effect here, the 75% overlap case was run at 90% applied load. Maximum principal strains were rendered for the posterior epicardial surface and regions of strain concentration were identified. The max principal strain, as well as contributing fiber components, was plotted as a function of time for these cases.
Changing compression initiation
A range of changes in the start time of applied uniform compressions was simulated to gauge the effects on the overall system. The base compression profile is the previous sinusoidal profile, with all circumferences compressing at the same time. Starting from the original 154 ms time, compression profiles were shifted by 10, 20, and 50 ms earlier and later in the cardiac cycle (Figure 1C). Thus, the earliest simulated compression started at 104 ms and the latest began at 204 ms. All these time points were run at 50% and 80% of the maximum load. 80% load was chosen to still interrogate the fiber dynamics above the 70% threshold previously established while also being more sensitive to the large timing changes investigated in these simulations. The hemodynamics for each force load were plotted for each start change. The maximum principal strain for each 80% load was rendered and displayed, along with the time that the maximum strain occurred and its value. Time series of the maximum principal strain and relevant fiber components were plotted for the two extremes of this parametric series.
Statistical analysis
Due to these experiments being a FEA, there are not statistical analysis that was done. Instead, error criterions are assigned to ensure convergence of the simulations. There criteria are: (I) the determinant of the deformation gradient, does not decrease past 0.95, ensuring an isochoric material, (II) the calculated volume change in the ventricular model and the lumped parameter model are less than epsilon, and (III) the left and right ventricular stroke volumes are within 5% of each other.
Results
Sequential compression
Hemodynamics
Four main hemodynamic metrics were analyzed for the sequential compressions: ejection fraction (EF), stroke volume (SV), peak pressure (PP), and end diastolic volume (EDV). These values were plotted for the 50% load case for each of the overlaps (25%, 50%, 75%, and 100%) (Figure 2).
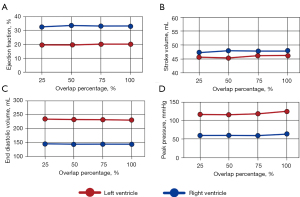
Across all hemodynamic parameters, there is very little change with the degree of overlap. Left and right ventricle ejection fractions maintained values between 19–20% and 32–33% respectively (Figure 2A). Similarly, stroke volume remained relatively unchanged with left and right ventricle values of 45–46 and 47 mL respectively (Figure 2B). Left ventricular (LV) diastolic volume decreased slightly with increasing overlap with 233.5 mL at 25% overlap and 230.6 mL at 100% overlap while right ventricular (RV) end diastolic volume ranged between 143 and 144 mL (Figure 2C). Peak pressure had the largest trend, with values increasing as the overlaps got larger. The LV peak pressure went from 115.1 to 123.5 mmHg while the RV followed suit, rising from 59.4 to 62.0 mmHg as the overlap increased from 25% to 100% (Figure 2D).
Surface renderings
The uniform compression and 75% overlap sequential compression, both at 90% load, were analyzed throughout the cardiac cycle to find the maximum epicardial principal strain. 90% load was selected as it gave the maximum increase in hemodynamics while achieving convergence of the simulations. This occurred at 264 and 303 ms for the uniform and sequential compression respectively. For both time points, epicardial strain renderings are shown for the 90% load uniform compression, 50% load 75% overlap sequential compression, and 90% load 75% overlap sequential compression (Figure 3).
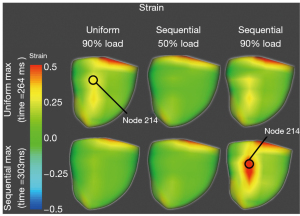
The 50% load has no visible strain concentrations at either of the time points. At the time point for the maximum strain in the uniform compression case (264 ms), there is a significant strain concentration near the posterior septum with a value around 0.32 Lagrange-Green strain (LG). This is maximum at node 214. At this same time point, the 90% load sequential simulation developed some strain concentration but not to the same extent or magnitude as the uniform compression. However, at time of maximum strain for the 90% load sequential compression (303 ms), there is a significant strain concentration in the same posterior location which affects more epicardium and has a much larger magnitude (around 0.58 LG) than the maximum strain in the uniform case. Moreover, the uniform case at 303 ms has no discernible strain concentrations.
Time series
Node 214, the location of the maximum strain for the uniform compression and the 75% overlap sequential compression at 90% load, were analyzed for the maximum principal strain and all fiber component strains throughout the last converged cardiac cycle (Figure 4).
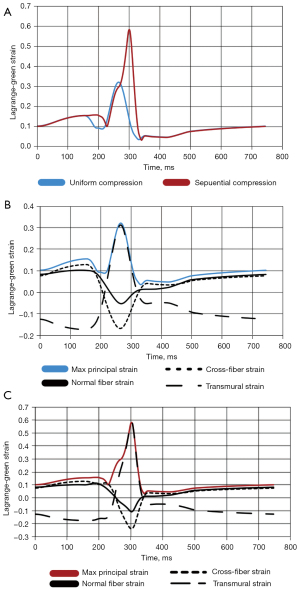
There is a substantial increase in the maximum principal strain going from uniform compression to sequential compression (0.32 vs. 0.58 LG) (Figure 4A). For uniform compression, the principal strain is primarily made up by the transmural strain during the applied compression. Before and after the compression, the principal strain mainly comprises the normal and cross-fiber strains. Additionally, there are substantial compressive strains in the fiber and cross fiber directions that occur with the applied compression (Figure 4B). This same situation is mirrored for the 90% load 75% overlap sequential simulation (Figure 4C). The main difference is the larger magnitudes for the principal and fiber components for the sequential compression compared to the uniform compression.
Changing compression initiation timing
Hemodynamics
The same four hemodynamic metrics that were examined for sequential compressions were also examined when applying uniform compression at differing starting points: ejection fraction, stroke volume, end diastolic volume, and peak pressure. These values are plotted against the change in start time for the 50% and 80% load cases (Figure 5). The decrease in end-diastolic volume with increased compression is expected as compression improves cardiac output with a set time for diastolic filling, given the set heart rate, and the compliance elements in the circulatory model.
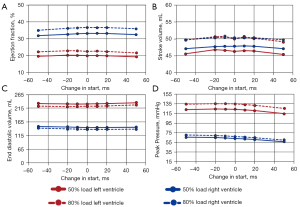
Across both loads (50% and 80%) the ejection fraction, stroke volume, and end diastolic volume are relatively unchanged as the start time changes. Peak pressure is the only parameter that has some discernable (albeit subtle) trend with start time change, decreasing as compressions start later (+50 ms) and increasing with earlier onset times (−50 ms). As the applied load increases from 50% to 80%, there are increases in ejection fraction, stroke volume, and peak pressure across all start time changes. Inversely, end diastolic volume decreases as the load increases across all changes in compression start times.
Left ventricle ejection fraction varied between 19–20% and 21–22% for the 50% and 80% loads respectively (Figure 5A). Similarly, the right ventricle ejection fraction ranged between 31–33% and 35–36% for the same loads. Stroke volume at 50% load ranged between 47.1–47.9 and 45.4–46.8mL for the RV and LV respectively. At 80% load, the stroke volumes were nearly identical between the LV and RV, with both ranging between 49.1–50.7 mL (Figure 5B). End diastolic volume ranged between 145–152 and 231–234 mL for the RV and LV respectively for the 50% load case (Figure 5C). Similarly, for the 80% load case, the EDV ranged between 137–142 and 220–226 mL for the RV and LV respectively. Peak pressure is the only metric that varied linearly with change in the start time. For the 50% load, peak pressure increased from 56.5–65.8 and 114.6–122.9 mmHg as the start time changed from + 50 to –50 ms, for the RV and LV respectively (Figure 5D). This trend was maintained for the 80% load case, with peak pressures increasing from 59.7–70.3 and 125.4–134.2 mmHg across the same change in start for the RV and LV respectively.
Surface renderings
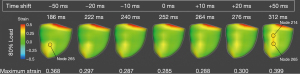
Maximum principal strain is rendered for the posterior epicardial surface for each change in compression start time (±50, 20, 10, and baseline) for the 80% load case (Figure 6). The time of each rendering is displayed above each image and was chosen based on when the maximum principal strain occurred in node 265, where the strain was concentrated. There is a trend between shifting the start of compression and the time of peak strain, with peak strain occurring earlier in the cardiac cycle as the start of compression shifts earlier. The time that peak strain occurs decreases from 312 to 186 ms as the start of compression shifts from +50 to −50 ms. From the epicardial renderings, there is a strain concentration on the posterior septum towards the apex, indicated by node 265. Progressing from −50 to +50 ms, a more basal concentration point develops above node 265. This strain concentration fully develops at +50 ms, with a vertical band of strain concentration on the posterior septum, with the two focal points at node 214 and 265. The maximum principal strain for node 265 is shown for all renderings. There is a parabolic trend with this strain. A minimum value of 0.285 LG exists at the baseline compression (0 ms). From this point, the strain increases as the start of compression is shifted earlier or later, with maximum values of 0.368 LG and 0.399 LG at −50 and +50 ms respectively.
Time series
The maximum principal strain as well as all relevant fiber components are plotted for the last converged cardiac cycle for node 265 for the −50 ms case and for nodes 214 and 265 for the +50 ms case (Figure 7). Examining node 265 for the −50 ms case, the cross-fiber normal strain dominates the principal strain before and after compression (Figure 7A). During compression, the cross fiber normal strain, fiber-cross fiber shear, and fiber-transmural shear strain all tend to compressive strain. The fiber-cross fiber and fiber transmural shear strains are neutral outside of compression whereas the cross-fiber normal strain reaches 0 strain during compression. Contrasting this, the transmural normal strain trends to extension strain, also reaching 0 during compression.
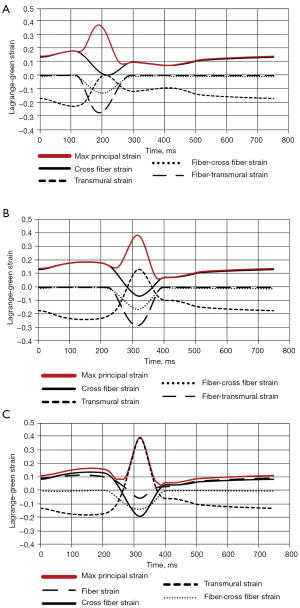
When examining node 265 for the +50 ms case, a starkly different dynamic is present (Figure 7B). The principal strain is mainly dominated by the cross fiber normal strain before and after the applied compression. However, during compression, the cross fiber normal strain as well as the fiber-cross fiber and fiber-transmural shear strains all become compressive while the transmural normal strain increases. All these contribute to the max principal strain during compression.
For node 214, there are substantial differences compared with node 265, despite them being both in the +50 ms case and in the same general area of strain concentration on the posterior epicardial surface (Figure 7C). The maximum principal strain is dominated by the transmural normal strain during compression. Before and after the applied compression, however, the maximum principal strain is comprised mostly of the fiber and cross fiber normal strains. Additionally, during the applied compression the fiber and cross fiber normal strains as well as the fiber- cross fiber shear strains become compressive.
Discussion
In this manuscript, we expand upon our group’s previous work and investigate the hemodynamic and regional mechanical responses of a patient-specific beating heart model to temporal and conformational changes in epicardial compression. We investigated this via two experiments: (I) changing the compression from uniform (all circumferences compressed at the same time) to sequential (compressing from the apex to the base) and (II) shifting the start of compression to be earlier or later in a set cardiac cycle at 80 beats per minute. While each experiment revealed unique dynamics, the overarching point to be made is as follows: while various compression schemes result in nearly identical hemodynamics, regional mechanics can differ substantially.
In the sequential compression simulations, circumferential compressions were timed so that the apex would compress first followed by the next basal circumference and so on (Video 1). There was no significant change in the hemodynamics for any of these delays for the 50% load case. This would imply that, clinically, any of these compression schemes would result in the same hemodynamics since there is natural variation from one heartbeat to the next in patients. The lack of difference in the hemodynamics is at odds with the taught method of manual cardiac compression, which is aimed at maximizing cardiac output. However, the main distinction between the two cases is that manual cardiac compression is reserved for cardiac arrest, with no actively contracting myocardium. As such, the fibers are not generating any force. In these simulations, the fibers are actively contracting and generating force, becoming stiffer as the more basal circumferences are compressed. Overall, the results for this patient-specific model suggest that changing compressions from uniform to sequential does not yield hemodynamic improvement, but significantly increased myocardial strain, suggesting that uniform compression would be the compression scheme of choice when dealing with active myocardium.
From a circulatory support perspective, shifting the start of uniform compressions has a similar affect as applying sequential compression profiles, with global hemodynamics being relatively unchanged across all tested start times. However, when the range of compression start times is analyzed, considerable differences in the resulting regional mechanics exist. Starting compression later or earlier in the cardiac cycle results in an increase in the principal strain, suggesting that a local minimum for the timing of cardiac compression exists. More interestingly, the fiber component dynamics change considerably. Between the earliest (−50 ms) and latest (+50 ms) compressions at node 265, there are similar magnitudes for the principal strains but differing component strains, altering the component makeup of the principal strain. In the −50 ms case, no one component is completely determining the principal strain during compression, were as in the +50 ms case, the transmural strain contributes significantly to the principal strain. Moreover, the differing fiber components show that compressing later in the cardiac cycle increases the magnitudes of strain, both compressive and extensive, in key components that are not the fiber strain. This is likely due to the interplay between the active state of the fibers and well as in the ventricular pressure during this compression.
Even more interesting are the different dynamics in the +50 ms case between nodes 214 and 265. While these are at the same start of compression and same time in the cardiac cycle, there are considerable differences: (I) in node 214, the principal strain during compression is primarily dominated by the transmural strain and (II) the principal strain before and after compression in node 214 are composed of the cross fiber and fiber strain. These results emphasize the importance of considering the topography of the compression. Additionally, the maximum principal strain is largely determined by the transmural strain for node 214 whereas in node 265, no specific component dominates. This suggests that if designing a compression profile for this patient’s heart, the applied compression node 214, and perhaps this circumference, should be decreased to avoid a substantial increase in the transmural strain, as the myocardium is much less stiff in this direction. This shows that even with similar maximum principal strains, the fiber components can differ significantly between locations in the myocardium.
All these results demonstrate the importance of timing DCC. Due to the changing stiffness of the actin-myosin interactions throughout the cardiac cycle, the transforming myocardial geometry, and the ventricular pressure, the resulting myocardial strain can change dramatically despite no commensurate change in the hemodynamic improvement. This points to the necessity of computational analysis for DCC.
Limitations
First and foremost, the main limitation in the study is a lack of validation of the simulations. While the baseline simulations have been validated against physiologic data, the intervention of DCC has not. Therefore, the results should be taken within this context. Moreover, there are three other limitations in this current study. The first is that a single patient specific model is used. As such, while specific recommendations can be made for compression profiles, larger overall considerations can only be suggested until more patient models are analyzed in a similar fashion and trends drawn. Further work is necessary to examine the robustness of these findings. The second limitation is the boundary conditions employed in this model. Fixed boundary conditions can heighten the biomechanics (stress/strain) and affect the overall hemodynamics of the simulations. Nevertheless, these effects would be unlikely to show such substantial differences as seen in this manuscript due to two reasons. The first is that the boundary conditions that are applied are similar the valvular plane and the fibrous skeleton of the heart in that movement is more restricted at that base. This would provide similar dynamics in-vivo as compared to in-silico. The second is that there is a visible decrease to the stain, to almost 0, before the strain concentration appears. in both experiments given that there is no overriding strain with a concentration near a fixed boundary condition. Moreover, a lack of any valves (e.g., mitral, aortic) and blood flow could also cause errors in the biomechanical assessment. While the lack of detailed valvular dynamics can lead to errors in the hemodynamic results, previous comparisons of these models to their human counterparts show good agreement with the ventricle hemodynamics (13). Lastly, these simulations were run for a single heart rate and future work will need to be done to analyze the effects of changing the timing of compressions in tandem with differing heart rates.
Conclusions
These simulation studies were performed to investigate the hemodynamic and biomechanical consequences of changing the temporal and conformational aspects of DCC. This was accomplished by changing compression profiles from uniform to sequential from apex to base as well as shifting the start of uniform compression earlier and later in the cardiac cycle. For both these conditions, we have shown that while global hemodynamics did not significantly vary throughout both experiments, the maximum principal strain concentrations and their respective fiber components did. This underscores the need for computational simulations of cardiac compression to help guide the design of customized compressive devices by quantifying the hemodynamic benefits and biomechanical consequences of DCC on a case-by-case basis.
Acknowledgments
Funding: None
Footnote
Data Sharing Statement: Available at https://shc.amegroups.com/article/view/10.21037/shc-21-24/dss
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://shc.amegroups.com/article/view/10.21037/shc-21-24/coif). LKW reports that he is the CEO of Insilicomed, whose software was used for this manuscript. No funding was received or given for this work. The other authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Virani SS, Alonso A, Benjamin EJ, et al. Heart Disease and Stroke Statistics-2020 Update: A Report From the American Heart Association. Circulation 2020;141:e139-e596. [Crossref] [PubMed]
- Alraies MC, Eckman P. Adult heart transplant: indications and outcomes. J Thorac Dis 2014;6:1120-8. [PubMed]
- Hsich EM. Matching the Market for Heart Transplantation. Circ Heart Fail 2016;9:e002679. [Crossref] [PubMed]
- Acharya D, Loyaga-Rendon R, Morgan CJ, et al. INTERMACS Analysis of Stroke During Support With Continuous-Flow Left Ventricular Assist Devices: Risk Factors and Outcomes. JACC Heart Fail 2017;5:703-11. [Crossref] [PubMed]
- Kirklin JK, Naftel DC, Pagani FD, et al. Seventh INTERMACS annual report: 15,000 patients and counting. J Heart Lung Transplant 2015;34:1495-504. [Crossref] [PubMed]
- Roche ET, Horvath MA, Wamala I, et al. Soft robotic sleeve supports heart function. Sci Transl Med 2017;9:eaaf3925. [Crossref] [PubMed]
- Han J, Kubala M, Trumble DR, editors. Design of a Muscle-Powered Soft Robotic Bi-VAD for Long-Term Circulatory Support. Minneapolis, Minnesota, USA: 2018 Design of Medical Devices Conference, 2018: V001T01A003.
- Hord EC, Bolch CM, Tuzun E, et al. Evaluation of the CorInnova Heart Assist Device in an Acute Heart Failure Model. J Cardiovasc Transl Res 2019;12:155-63. [Crossref] [PubMed]
- Han J, Kubala M, Aranda-Michel E, et al. Ventricle-specific epicardial pressures as a means to optimize direct cardiac compression for circulatory support: A pilot study. PLoS One 2019;14:e0219162. [Crossref] [PubMed]
- Aranda-Michel E, Waldman LK, Trumble DR. Left ventricular simulation of cardiac compression: Hemodynamics and regional mechanics. PLoS One 2019;14:e0224475. [Crossref] [PubMed]
- Aranda-Michel E, Waldman LK, Trumble DR. Computational methods for parametric evaluation of the biventricular mechanics of direct cardiac compression. Artif Organs 2021;45:E335-48. [Crossref] [PubMed]
- Kerckhoffs RC, Neal ML, Gu Q, et al. Coupling of a 3D finite element model of cardiac ventricular mechanics to lumped systems models of the systemic and pulmonic circulation. Ann Biomed Eng 2007;35:1-18. [Crossref] [PubMed]
- Krishnamurthy A, Villongco CT, Chuang J, et al. Patient-Specific Models of Cardiac Biomechanics. J Comput Phys 2013;244:4-21. [Crossref] [PubMed]
- Wise D, Davies G, Coats T, et al. Emergency thoracotomy: "how to do it Emerg Med J 2005;22:22-4. [Crossref] [PubMed]
Cite this article as: Aranda-Michel E, Waldman LK, Trumble DR. Exploring the timing and distribution effects of direct cardiac compression in a beating heart model. Shanghai Chest 2022;6:1.


